“In geometry and physics, spinors /spɪnər/ are elements of a complex number-based vector space that can be associated with Euclidean space.[b] A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation,[c] but unlike geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the “square roots” of vectors (although this is inaccurate and may be misleading; they are better viewed as “square roots” of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become “square roots” of differential forms).”
EXPLAIN!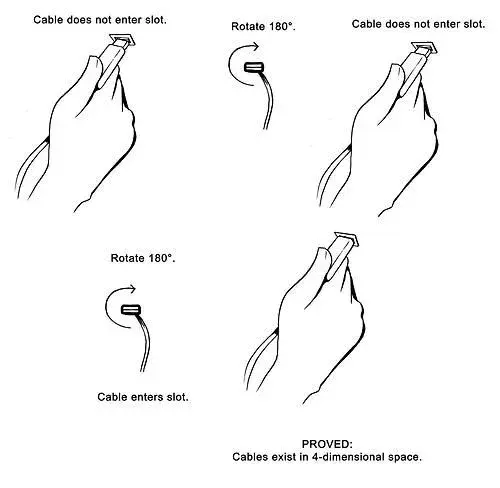
The picture explains itself. The cable exists in a 4-dimensional space.
The reply is pretty self-explanatory too. The cable exists in a 4-dimensional space.
You guys joke about this, but he managed to create a connector with three sides: up, down, and “oh yeah the first side was the correct one”
It doesn’t necessarily need to be 4-dimensional https://en.m.wikipedia.org/wiki/Spinor
That entry needs a ELI.
“In geometry and physics, spinors /spɪnər/ are elements of a complex number-based vector space that can be associated with Euclidean space.[b] A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation,[c] but unlike geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the “square roots” of vectors (although this is inaccurate and may be misleading; they are better viewed as “square roots” of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become “square roots” of differential forms).”
Seems pretty self-explanatory to me! /s
deleted by creator
USB-A is a spin-half connector type
Purged by creator