Here is a question I encountered sometime ago.
For a current carrying wire of finite length the value of B is less than that of an infinitely long wire (u can look up online for formulae or their derivation) at a same distance from the wire. So consequently the circulation of B on the path shown falls short of the value u times i. The biot savart law suggests the equation written above. The puzzle is to find the mistake.

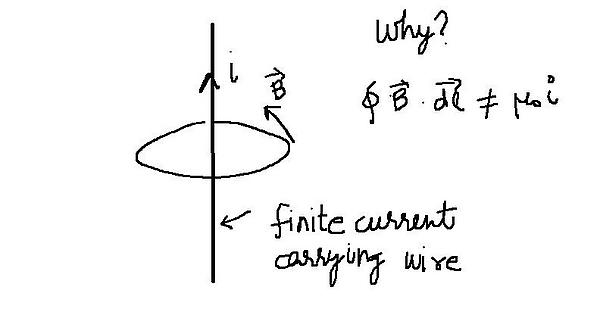
Well I suppose a cheesy way of putting this is that there is no such thing as a “current carrying wire of finite length”, by itself.
To expand, just because one can calculate the contribution to the magnetic field at some spatial point from such an object, doesn’t mean it is the sole source of the field in a theoretically consistent manner. If you complete the “loop” with two semi-infinite horizontal wires, and another vertical wire at infinity (assuming it has an emf there to power the circuit), then the field will change due to the two horizontal wires. This construction however breaks rotational symmetry around the original wire (so you’ll not be able to compute the loop integral simply as B times circumference), and in order to restore that, instead of just two horizontal wires, you’ll have to have infinite such pairs in all radial directions (like a squeezed coaxial cable). Anyway, I guess the point is after “completing the circuit”, the “paradox” will no longer be there.